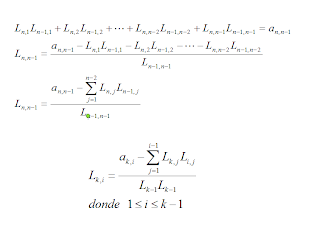Matrices are rectangular sets of elements represented by a single symbol. If the set if horizontal it is called row, and if it is vertical, it is called column.

There are some special types of matrices:
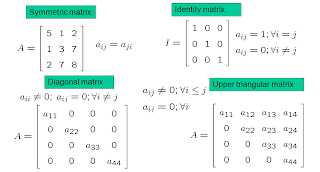
All elements are null with the exception of thoise in a band centered around the main diagonal. This matrix has a band width of 3 and has the name of tridiagonal.



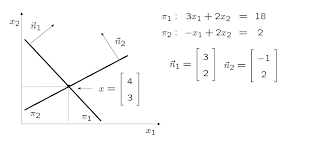
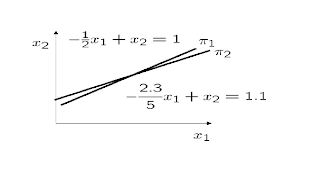
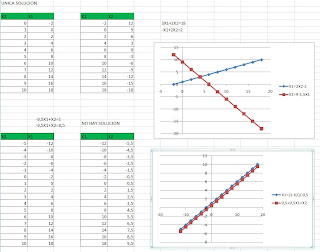
Graphic Solution: Systems of equations are hyperplanes (straight lines, planes, etc.). The solution of a system is the intersection of these hyperplanes.
Compatible and determined system. Vectors are linearly independent. Unique solution. Determinant of A is non-null.
Incompatible system, Linearly dependent vectors. Null determinant of A. There is no solution.
Compatible but undetermined system. Linearly dependent vectors. Null determinant of A. There exists an infinite number of solutions.
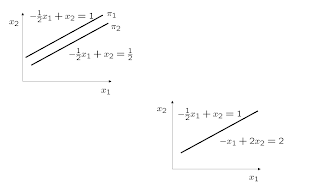
Compatible and determined system. Linearly independent vectors. Nonnull determinant of A, but close to zero. There exists a solution but it is difficult to find precisely. It is an ill conditioned system leading to numerical errors.

Gauss elimination
Naive Gauss elimination method: The Gauss’ method has two phases: Forward elimination and backsustitution. In the first, the system is reduced to an upper triangular system:
First, the unknown x1 is eliminated. To this end, the first row is multiplied by -a21/a11 and added to the second row. The same is done with all other succesive rows (n-1 times) until only the first equation contains the first unknown x1.
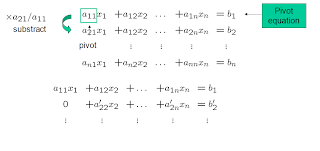
This operation is repeated with all variables xi, until an upper triangular matrix is obtained.
Next, the system is solved by backsustitution.
The number of operations (FLOPS) used in the Gauss method is:
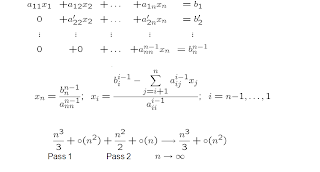
Forward Elimination (Row Manipulation):
a. Form augmented matrix [A|b]:
b. By elementary row manipulations, reduce [A|b] to [U|b'] where U is an upper triangular matrix:

Back Substitution
Solve the upper triangular system [U]{x} = {b´}

EXAMPLE:
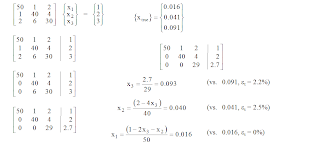

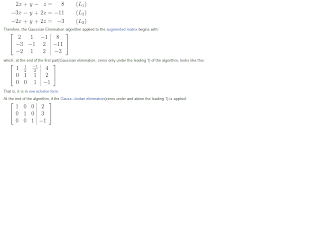
Gauss-Jordan Elimination
Diagonalization by both forward and backward elimination in each column.
Perform elimination both backwards and forwards until:
Operation count for Gauss-Jordan is:
(slower than Gauss elimination)


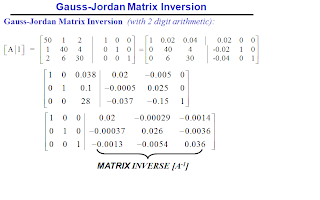
Gauss-Jordan Matrix Inversion
The solution of: [A]{x} = {b} is: {x} = [A]-1{b}
where [A]-1 is the inverse matrix of [A]
Consider: [A] [A]-1 = [ I ]
1) Create the augmented matrix: [ A | I ]
2) Apply Gauss-Jordan elimination:
==> [ I | A-1 ]

LU DESCOMPOSITION
LU decomposition - The LU decomposition is a method that uses the elimination techniques to transform the matrix A in a product of triangular matrices. This is specially useful to solve systems with different vectors b, because the same decomposition of matrix A can be used to evaluate in an efficient form, by forward and backward sustitution, all cases.
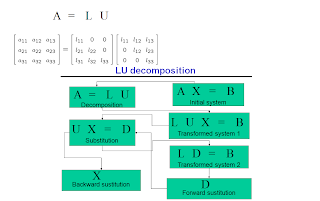

LU decomposition is very much related to Gauss method, because the upper triangular matrix is also looked for in the LU decomposition. Thus, only the lower triangular matrix is needed.
Surprisingly, during the Gauss elimination procedure, this matrix L is obtained, but one is not aware of this fact. The factors we use to get zeroes below the main diagonal are the elements of this matrix L.


The Gauss-Seidel Method
We are considering an iterative solution to the linear system
where is an sparse matrix, x and b are vectors of length n, and we are solving for x. Iterative solvers are an alternative to direct methods that attempt to calculate an exact solution to the system of equations. Iterative methods attempt to find a solution to the system of linear equations by repeatedly solving the linear system using approximations to the vector. Iterations continue until the solution is within a predetermined acceptable bound on the error.
Common iterative methods for general matrices include the Gauss-Jacobi and Gauss-Seidel, while conjugate gradient methods exist for positive definite matrices. Critical in the choice and use of iterative methods is the convergence of the technique. Gauss-Jacobi uses all values from the previous iteration, while Gauss-Seidel requires that the most recent values be used in calculations. The Gauss-Seidel method generally has better convergence than the Gauss-Jacobi method, although for dense matrices, the Gauss-Seidel method is inherently sequential. Better convergence means fewer iterations, and a faster overall algorithm, as long as the strict precedence rules can be observed. The convergence of the iterative method must be examined for the application along with algorithm performance to ensure that a useful solution to can be found.


GAUSS SEIDEL SUCCESSIVE OVER-RELAXATION
In numerical linear algebra, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process


Jacobi Method
Matrix diagonalization is the process of taking a square matrix and converting it into a special type of matrix--a so-called diagonal matrix--that shares the same fundamental properties of the underlying matrix. Matrix diagonalization is equivalent to transforming the underlying system of equations into a special set of coordinate axes in which the matrix takes this canonical form. Diagonalizing a matrix is also equivalent to finding the matrix's eigenvalues, which turn out to be precisely the entries of the diagonalized matrix. Similarly, the eigenvectors make up the new set of axes corresponding to the diagonal matrix.

Thomas Method
This method emerges as a simplification of an LU factorization of a tridiagonal matrix.
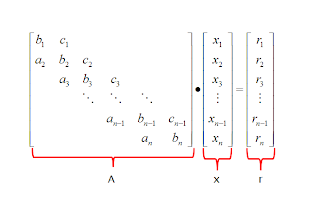
Saying that A = LU and applying Doolittle where Lii = 1 for i = 1 to n, we get:
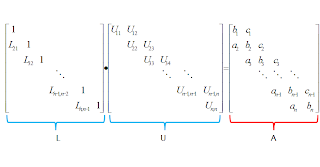
Based on the matrix product shown above gives the following expressions:
As far as making the sweep from k = 2 to n leads to the following
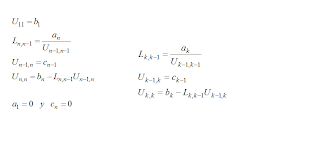
If Lux and Ux = r = d then Ld = r, therefore:
So from a progressive replacement
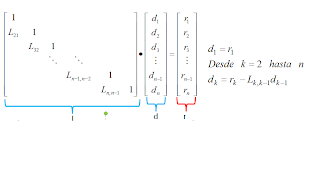
Finally we solve Ux = da from a backward place
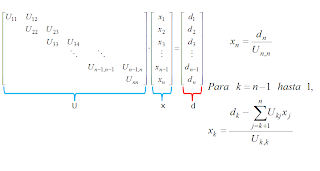


Cholesky method
As LU factorization method is applicable to a positive definite symmetric matrix and where:
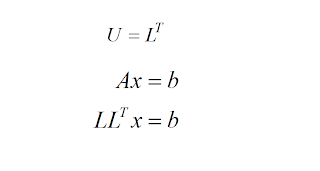
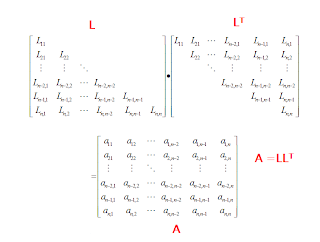
From the product of the n-th row of L by the n-th column of LT we have:
Making the sweep from k = 1 to n we have:

On the other hand if we multiply the n-th row of L by the column (n-1) LT we have:
By scanning for k = 1 to n we have: