CALCULATION OF ROOTS OF EQUATIONS
METHOD OF BISECTION

It is the oldest and most basic method of finding the roots of an equation. Is directly based on the theorem of Bolzano explained above. Involves taking an interval [x0, x1] such that f (x0) f (x1) <0,> Maxit), in which case you need to print an error message indicating that the method does not converge.

Two operations represented in the diagram in figure (3) require additional explanation:

The midpoint of the interval is calculated as in the workplace. It thus follows an overall strategy to make numerical calculations indicating that it is better to calculate a term adding a small amount of correction to a previously obtained approximation. For example, in a computer of limited accuracy, there are values x0 and x1 for which xm is calculated by leaving the interval [x0, x1].
The convergence () is calculated using the expression. Thus, the term represents the number of significant figures with which we obtain the result.

METHOD OF SUCCESSIVE APPROXIMATIONS


Given the equation f (x) = 0, the method of successive approximations replaced by an equivalent equation, x = g (x), defined in the form g (x) = f (x) + x. To find the solution, we start with an initial value x0 and compute a new approach x1 = g (x0). We replace the new value obtained and repeat the process. This leads to a succession of values, if it converges, will limit the solution of the problem.



















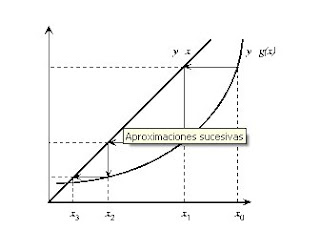
Figure (4) shows the geometric interpretation of the method. We start from an initial point x0 and compute y = g (x0). The intersection of this solution with the line y = x will give a new value x1 closer to the final solution.

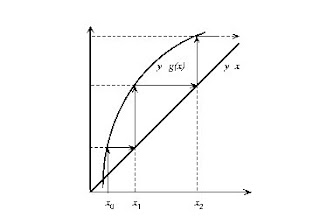
However, the method can easily diverge. It is easy to verify that the method can only converge if the derivative g '(x) is smaller in absolute value than unity (the slope of the line defined by y = x). An example of this case is shown in Figure (5). This condition, which a priori can be considered a severe restriction of the method, can be ignored easily. It is sufficient to choose the function g (x) as follows:


so that taking a proper value, we can always make g (x) satisfies the condition of the derivative.

















NEWTON METHOD


This method is part of an initial approximation x0 and obtains a better approximation, x1, given by the formula:
(29)


The above expression can be derived from a Taylor series expansion. Indeed, let r be a zero of f and an approximation ar x such that r = x + h. If f''exists and is continuous, by Taylor's theorem we have:


0 = f (r) = f (x + h) = f (x) + hf '(x) + O (h2) (30)


where h = r-x. If x is near ar (hes ie small), it is reasonable to ignore the term O (h2):


0 = f (x) + hf '(x) (31)


so we get the following expression for h:

(32)


From equation (32) and taking into account that r = x + h is easy to derive the equation.
















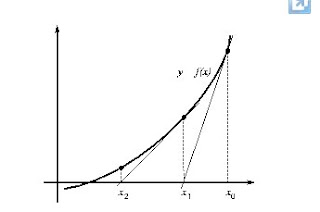
Newton's method has a simple geometric interpretation, as can be seen from the analysis of the figure (6). In fact, Newton's method is a linearization of the function, ie f is replaced by a line that contains the point (x0, f (x0)) and whose slope coincides with the derivative of the function at the point , f '(x0). The new approach to the root, x1, is obtained from the intercept of the linear function with the X-axis of ordinates.




Let's see how we can obtain equation (29) from what is said in the previous paragraph. The equation of the line through the point (x0, f (x0)) and slope f '(x0) is:


and - f (x0) = f '(x0) (x-x0) (33)


where, with y = 0 and solving for x we obtain the Newton-Raphson equation (29).









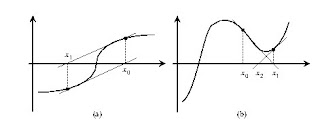
Newton's method is very fast and efficient since the convergence is quadratic (the number of significant digits doubles at each iteration). However, the convergence depends heavily on the form that function in the vicinity of the iteration. are two situations in which this method is not able to achieve convergence or converge to a point that is not a zero of the equation.




SECANT METHOD

The main disadvantage of Newton's method is that it requires knowing the value of the first derivative of the function at the point. However, the functional form of f (x) sometimes hampers the calculation of the derivative. In these cases it is more useful to use the secant method.
The secant method from two points (and not just one as the Newton method) and estimates the tangent (ie, the slope of the line) by an approach according to the expression:

(34)




Substituting this in equation (29) of Newton's method, we obtain the expression of the secant method gives us the next iteration point:

















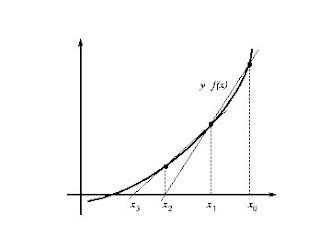
In the next iteration, we use the points x1 and x2para estimate a new point closer to the root of Eq (35). In figure (8) this method is represented geometrically.

In general, the secant method has the same advantages and limitations of the Newton-Raphson method described above.


METHOD OF FALSE POSITION



The method of false position is intended to combine the security of the bisection method with the speed of the secant method. This method, as with the bisection method stems from two points surrounding the root f (x) = 0, ie, two points x0 and x1tales that f (x0) f (x1) <0. The following approach, x2, is calculated as the X axis intersection with the line joining two points (using equation (35) of the secant method). The allocation of the new search interval is as in the bisection method: between the two intervals, [x0, x2] and [x2, x1], take that which satisfies f (x) f (x2) <0. Figure (9) is represented geometrically this method.















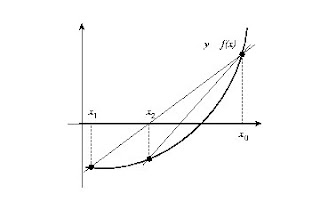
The choice guided the range represents an advantage over the secant method as it inhibits the possibility of a divergence of method. On the other hand and regarding the bisection method, greatly improves the choice of the interval (and not merely from the interval by half).










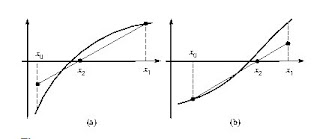
However, the method of false position has a very slow convergence towards the solution. Indeed, after starting the iterative process, one end of the interval tends to change (see Figure (9)). To circumvent this problem, we proposed a modification of the method, called Hamming method. Under this method, the approximation to a root is from the determination of the X axis intersection with the line joining the points (x0, f (x0) / 2) and (x1, f (x1)) if the function is convex in the interval or from the line joining the points (x0, f (x0)) and (x1, f (x1) / 2) if the function is concave in the interval. Figure (10) is plotted the Hamming method.




As mentioned, the Hamming method required to determine the concavity or convexity of the function in the interval of iteration. A relatively simple method to determine the curvature of the function is to evaluate the function at the midpoint of the interval, f (xm) (where xm is calculated as the bisection method).